Project Euler problem 37: Truncatable primes

I had some fun with problem 37 in project Euler. The problem description states the following:

The number 3797 has an interesting property. Being prime itself, it is possible to continuously remove digits from left to right, and remain prime at each stage: 3797, 797, 97, and 7. Similarly we can work from right to left: 3797, 379, 37, and 3.

Find the sum of the only eleven primes that are both truncatable from left to right and right to left.

NOTE: 2, 3, 5, and 7 are not considered to be truncatable primes.

First I solved this problem using the method that many followed, which is to start with a list of primes, and eliminate all primes that are not truncatable. This approach turned out to be quite slow (admittedly, my trying to do it in Excel did not help), and problematic on one critical point. How large should your largest prime be. There is no clear mechanism to prove what the maximum possible bidirectionally truncatable prime could be. Except looking it up on Wikipedia. In fact, Excel was not really able to handle the number of lines that turned out to be required, as most people use a million primes.

A nicer solution

Actually, playing around out of dissatisfaction, I stumbled upon the way to actually prove the absolute number of bidirectionally truncatable primes, using the following thought process:

1. A bidirectionally truncatable prime is both right-truncatable and left-truncatable.
2. Right-truncatable and left-truncatable primes may be constructed by a stepwise process adding one digit at a time and testing for primality.
3. It can be proven when the maximum right- and left-truncatable primes have been found: the addition of the next digit does not deliver any primes.
4. Because of point 2, this means that the intersection of left- and right-truncatable primes will probably have a finite size.

This approach needs no assumptions on the maximum size of the primes, and turns out to be very fast because of the stepwise algorithm, when a speedy primality test is used.

The algorithm itself

The algorithm itself is really simple:

~~~ python rtrunc_primes = rtrunc_primes() ltrunc_primes = ltrunc_primes()

tprimes = sorted(list(rtrunc_primes & ltrunc_primes))

We simply get all right truncatable primes, all left truncatable primes and use the set intersection operator `&` to get our answers. I make a sorted list in order to be able to drop the first 4 primes in the summation, as that is how [Project Euler problem 37][Euler37] is stated.


I get the answer and the list of primes using these simple statements:

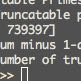
```python
print "Truncatable primes: ", tprimes
print "Sum minus 1-digit primes: ", sum(tprimes[4:])
print "Number of truncatable primes: ", len(tprimes)

Generating the right truncatable primes

Generating the right truncatable primes is the easy part.

We have to consider that the 1-digit right truncatable primes are simply the 1-digit primes, that any additional digit needs to be a valid last digit for a prime and that the whole number must be prime. Since all primes above 9 end on either a 1, 3, 7 or 9, this really reduces the number of tests required. Even without optimization this runs really quickly on modern systems. After some rewriting (still learning to use the list comprehensions in Python), this is my result:

from itertools import chain
 
def rtrunc_primes():
  """Generate a set of all right-truncatable primes"""
  rprimes = [[2, 3, 5, 7]] # Seed with 1-digit primes
  rdigits = [1, 3, 7, 9] # Only possible digits after first digit
 
  n = 2
  while rprimes[n-2]: # Continue as long as we have found a prime in the previous n
    nprimes = [p for base in rprimes[n-2] for p in [10*base+d for d in rdigits ] if is_prime (p)]
    rprimes.append(nprimes)
    n += 1
  return {p for p in chain.from_iterable(rprimes)}

Generating left truncatable primes

The left truncatable primes are slightly more difficult. But following the same logic, we start with the one-digit primes, then continue adding digits to the left until we no longer find a prime for a given digit length. So glad that Python does away with old-fashioned maximum limits on ineger sizes. In this case, there are more primes and the number of possible digits is larger, but still it runs in a blink of an eye on my systems.

def ltrunc_primes():
  """Generate a set of all left-truncatable primes"""
  lprimes = [[2, 3, 5, 7]] # Seed with 1-digit primes
  ldigits = range(1,10) # Only possible digits after first digit
 
  n = 2
  factor = 1
  while lprimes[n-2]: # Continue as long as we have found a prime in the previous n
    factor *= 10 # We need to stick the digits to the front, so mult with factor
    nprimes = [p for base in lprimes[n-2] for p in [base + l * factor for l in ldigits] if is_prime(p)]
    lprimes.append(nprimes)
    n += 1
  return {p for p in chain.from_iterable(lprimes)}

Implementation of the primality test

Others have done a great job in coming up with all kinds of primality tests. Not being an expert, I used the force and found a perfectly suitable solution. It may not have been proven up to the large numbers that end up being in the left-truncatable set, but it gives the correct result. In the end, the algorithm turns out to be correct, and would still be with a more rigorous primality test. This is the test that I pretty much just copied.